Calculating chance - the rules of probability

Calculating chance or working out probabilities can be remarkable simple - or extremely complicated. Much depends on what kind of probabilities you are trying to work out: dependent or independent.

Dependent probabilities deal with events that affect subsequent events, for example drawing different colored balls from a bag on which each ball pulled out alters the numbers left inside. These are more complicated to compute so in this article, I'll take a look at independent probabilities: the chances of a coin coming down heads or tails or a dice landing on a particular number.

Coins and dice have no memory (although dice can be 'loaded', more of which later). This means that the probabilities remain essentially constant throughout a series of 'events' - flips of the coin or throws of the dice.

The formula for working out an independent probability is quite simple:

P(A) = N/0

where

P(A) equals Probability of any event occurring
N is the Number of ways an event can occur and
0 is the total number of possible Outcomes.

Let's first test that on the toss of a coin.

Coin flips

Heads or tails?

It's obvious that the chances of a normal two-sided coin coming down heads, rather than tails, are exactly 50/50 for each throw. The coin can only land on one side or the other (event) but there are two possible outcomes: heads or tails. One over two is a half, or 50 per cent.

What's not so obvious is that the probability of a coin that has come up heads for the past 19 flips also landing heads up on the 20th throw is also 50 per cent.

You might object that such an event would be most unlikely - and you'd be right. Nevertheless, looked at logically, you can see that the 'unprecedented' event has already happened on each of the previous flips when the coin came up heads again. So, at each new spin the probabilities reset. The coin has no memory and each event has no effect on the next.

The same formula, P(A) =  N/0, applies when tossing more than one coin and calculating chances of particular events. Now the number of possible outcomes is that for each object, raised to the power of the number of objects.

Thus with one coin there were two outcomes (H/T) but with two coins there will be four (2²) permutations, which can be seen as TT, HT, TH, HH. With three coins, there will be eight possible outcomes (2x2x2).

Note that in calculating probabilities it is necessary to keep each outcome separate, even when they seem to be the same. Coin A showing Heads while Coin B shows tails is NOT the same outcome as the two coins coming down the other way round.

If we want to know the probability that one of three coins tossed will come down tails, we can see that there are three ways in which that event can occur, that it will be Coin A, Coin B, or Coin C that shows tails, or to put in binary form, THH, HTH, or HHT. Therefore the probability is three-eighths, or 37.5 per cent.

Tails-Heads-Heads
Tails-Tails-Heads
Tails-Tails-Tails
Tails-Heads-Tails
Heads-Tails-Heads
Heads-Tails-Tails
Heads-Heads-Tails
Heads-Heads-Heads

But the chance of all three coins showing tails is much less. There is only one TTT event, so the probability is one in eight or 13 per cent.

Calculating dice probabilities

Essentially, the same formula applies to dice - but calculating the probabilities is much more complex.

Plainly the probability of rolling a six with a single six-sided dice (I never say 'die') is one event in which it lands with six uppermost, divided by six possible outcomes from a single throw, or one sixth (16.66 per cent).

Now it might seem that that chances of throwing two sixes with two dice might also be one sixth (two six faces divided by a total of 12 faces) but this is to misunderstand the meaning of 'outcomes'.

Multiple dice

There are actually 36 possible outcomes from throwing a pair of six sided dice, listed below:

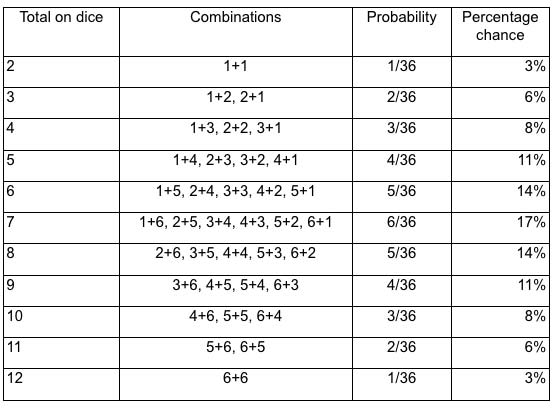
So the chances of throwing a two, 12 or any other chosen 'double' is only 1/36, or around 3 per cent.

Again, the number of possible outcomes is the number of those for each dice, raised to the power of the number of dice in play. So with two dice, that's 6² = 36. Again, there is only one type of event in which both dice show the same particular number, so 1/36.

I say 'particular' number because the chances of throwing any 'double' are different. There are six ways in which that event can happen (1+1, 2+2, etc.) so the probability of throwing a double is 6/36, or one sixth.

And what about the chances of a particular number, say five, coming up on at least one of the two dice? Well, if the probability of throwing a five on one dice is 16.6 per cent, you might assume that it's twice as likely (33.3 per cent) to happen when doubling the number of dice. But that wouldn't be exactly correct. There are six possible events in which Dice A shows a five and six more where the five shows on Dice B. That's 12 events out of 36 but one of those is shared between both dice (the double five) so the actual number of events is 11, and so the probability is slightly reduced to 11/36, or around 30 per cent.

Rule of One

Another way to work out the probabilities is the Rule of One. Plainly there is total certainty (1/1 or 100 per cent) that the dice will either end up showing a five or not. Therefore the chances of no five showing on two dice are 36/36 minus 11/36, which is 25/36. Subtracting the probabilities of any given event from one always tells you the chances of the opposite occurring.

This 'back to front' method becomes more useful as the number of dice increase. As an example, it would be quite hard, when rolling four dice, to work out the chances of one of the dice showing four or less.

But it's relatively easy to work out the reverse case that all the dice end up fives or sixes. That would be a 1/3 chance on each dice, raised to the power of four. So 1/3 x 1/3 x 1/3 x 1/3 is 1/81. When you take that away from one, that means a 80/81 chance that at least one of the dice will come up four or less.

In a future article, we'll take a look at working out the probabilities on dependent events, which may even include the chances of that elusive number 13 lottery ball coming out next onto the rack!

Your questions: