Compound Interest Calculator
- Compound Interest
- Simple Interest
- Daily Compound
- Forex Compound
Interest calculation for 5 years
$6,416.79 Total interest earned
$1,416.79 Initial balance
$5,000.00
28.34% The RoR represents the profit or loss % returned from your investment over the entire investment term. Learn more.
13 years, 11 months
Interest rate:5% yearly
Effective Rate:5.12%
Compounding:Monthly
- Start investing early.
- Make regular contributions if possible.
- Consider tax-efficient savings products with more frequent compounding.
- What is compound interest? | Investing for compound interest
| Month | Deposits & Withdrawals | Interest | Total Deposits & Withdrawals | Accrued Interest | Balance |
|---|---|---|---|---|---|
| 0 | $5,000.00 | – | $5,000.00 | – | $5,000.00 |
| 1 | $20.83 | $20.83 | $5,020.83 | ||
| 2 | $20.92 | $41.75 | $5,041.75 | ||
| 3 | $21.01 | $62.76 | $5,062.76 | ||
| 4 | $21.09 | $83.86 | $5,083.86 | ||
| 5 | $21.18 | $105.04 | $5,105.04 | ||
| 6 | $21.27 | $126.31 | $5,126.31 | ||
| 7 | $21.36 | $147.67 | $5,147.67 | ||
| 8 | $21.45 | $169.12 | $5,169.12 | ||
| 9 | $21.54 | $190.66 | $5,190.66 | ||
| 10 | $21.63 | $212.28 | $5,212.28 | ||
| 11 | $21.72 | $234.00 | $5,234.00 | ||
| 12 | $21.81 | $255.81 | $5,255.81 | ||
| 13 | $21.90 | $277.71 | $5,277.71 | ||
| 14 | $21.99 | $299.70 | $5,299.70 | ||
| 15 | $22.08 | $321.78 | $5,321.78 | ||
| 16 | $22.17 | $343.96 | $5,343.96 | ||
| 17 | $22.27 | $366.22 | $5,366.22 | ||
| 18 | $22.36 | $388.58 | $5,388.58 | ||
| 19 | $22.45 | $411.03 | $5,411.03 | ||
| 20 | $22.55 | $433.58 | $5,433.58 | ||
| 21 | $22.64 | $456.22 | $5,456.22 | ||
| 22 | $22.73 | $478.95 | $5,478.95 | ||
| 23 | $22.83 | $501.78 | $5,501.78 | ||
| 24 | $22.92 | $524.71 | $5,524.71 | ||
| 25 | $23.02 | $547.73 | $5,547.73 | ||
| 26 | $23.12 | $570.84 | $5,570.84 | ||
| 27 | $23.21 | $594.05 | $5,594.05 | ||
| 28 | $23.31 | $617.36 | $5,617.36 | ||
| 29 | $23.41 | $640.77 | $5,640.77 | ||
| 30 | $23.50 | $664.27 | $5,664.27 | ||
| 31 | $23.60 | $687.87 | $5,687.87 | ||
| 32 | $23.70 | $711.57 | $5,711.57 | ||
| 33 | $23.80 | $735.37 | $5,735.37 | ||
| 34 | $23.90 | $759.27 | $5,759.27 | ||
| 35 | $24.00 | $783.26 | $5,783.26 | ||
| 36 | $24.10 | $807.36 | $5,807.36 | ||
| 37 | $24.20 | $831.56 | $5,831.56 | ||
| 38 | $24.30 | $855.86 | $5,855.86 | ||
| 39 | $24.40 | $880.26 | $5,880.26 | ||
| 40 | $24.50 | $904.76 | $5,904.76 | ||
| 41 | $24.60 | $929.36 | $5,929.36 | ||
| 42 | $24.71 | $954.07 | $5,954.07 | ||
| 43 | $24.81 | $978.87 | $5,978.87 | ||
| 44 | $24.91 | $1,003.79 | $6,003.79 | ||
| 45 | $25.02 | $1,028.80 | $6,028.80 | ||
| 46 | $25.12 | $1,053.92 | $6,053.92 | ||
| 47 | $25.22 | $1,079.15 | $6,079.15 | ||
| 48 | $25.33 | $1,104.48 | $6,104.48 | ||
| 49 | $25.44 | $1,129.91 | $6,129.91 | ||
| 50 | $25.54 | $1,155.45 | $6,155.45 | ||
| 51 | $25.65 | $1,181.10 | $6,181.10 | ||
| 52 | $25.75 | $1,206.86 | $6,206.86 | ||
| 53 | $25.86 | $1,232.72 | $6,232.72 | ||
| 54 | $25.97 | $1,258.69 | $6,258.69 | ||
| 55 | $26.08 | $1,284.77 | $6,284.77 | ||
| 56 | $26.19 | $1,310.95 | $6,310.95 | ||
| 57 | $26.30 | $1,337.25 | $6,337.25 | ||
| 58 | $26.41 | $1,363.65 | $6,363.65 | ||
| 59 | $26.52 | $1,390.17 | $6,390.17 | ||
| 60 | $26.63 | $1,416.79 | $6,416.79 |
| Year | Deposits & Withdrawals | Interest | Total Deposits & Withdrawals | Accrued Interest | Balance |
|---|---|---|---|---|---|
| 0 | $5,000.00 | – | $5,000.00 | – | $5,000.00 |
| 1 | $255.81 | $255.81 | $5,255.81 | ||
| 2 | $268.90 | $524.71 | $5,524.71 | ||
| 3 | $282.65 | $807.36 | $5,807.36 | ||
| 4 | $297.12 | $1,104.48 | $6,104.48 | ||
| 5 | $312.32 | $1,416.79 | $6,416.79 |
Use our free compound interest calculator to evaluate how your savings or investments might grow over time, with or without regular contributions. Our tool provides both monthly and yearly interest projections, helping you see how compound interest can increase the value of your money as you plan for the future. Got questions? Just ask. Continue scrolling to learn how compound interest works – and how to make it work for you.👇
Disclaimer: Whilst every effort has been made in building our calculator tools, we are not to be held liable for any damages or monetary losses arising out of or in connection with their use. Full disclaimer.
What is compound interest?
The concept of compound interest, or 'interest on interest', is that accumulated interest is added back onto your principal sum, with future interest being calculated on both the original principal and the already-accrued interest.
This compounding effect causes investments to grow faster over time, much like a snowball gaining size as it rolls downhill.
Unlike simple interest, which is calculated only on the principal, compound interest is calculated on both the principal and the accumulated interest. This is what makes it so powerful for long-term growth.
When you then start introducing regular, consistent investing over a sustained period of time, the effects of compound interest are amplified, giving you a highly effective growth strategy for accelerating the long-term value of your savings or investments.
To illustrate the effect of compounding, let's take a look at an example chart of an initial $1,000 investment. We'll use a 20 year investment term at a 10% annual interest rate (just for simplicity). As you compare the compound interest line to those for standard interest and no interest at all, you can see how compounding boosts the investment value.
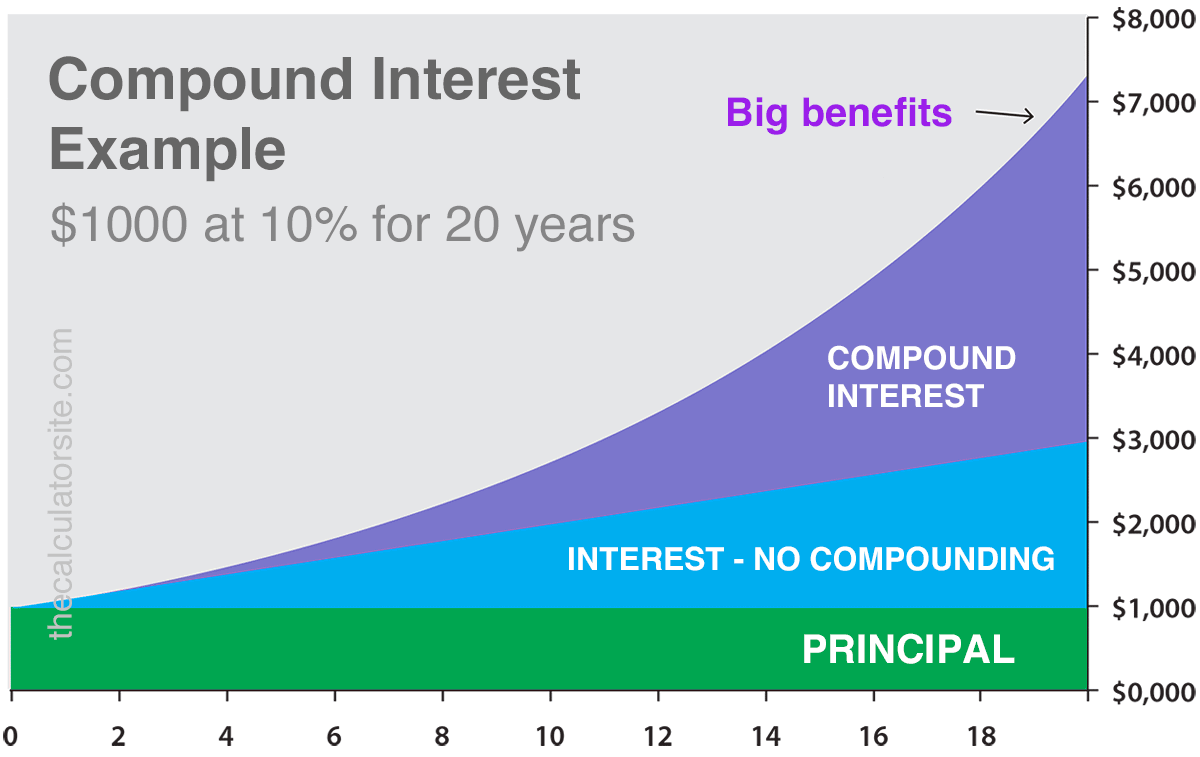
So, how important is compound interest? Just ask Warren Buffett, one of the world's most successful investors:
Warren Buffett 5
Making compound interest work for you
We've covered what compound interest is, but how do you make the most of it? Here are a few strategies to keep in mind:
- Start Early: Time plays an important role in compound interest. So, starting your investments early, even with smaller amounts, gives your money more time to grow and for the interest to compound.
- Regular Contributions: By consistently adding to your investment, you enhance the compounding effect (think about the analogy of a snowball). Each new contribution starts earning its own interest, adding to the overall growth.
- Higher Compounding Frequencies: When evaluating savings or investment options, pay attention to those that compound more frequently. The more often interest is compounded, the greater the potential for growth (although the difference may be minimal at lower interest rates).
Three simple strategies to consider when doing your long-term financial planning.
Where to invest for compound interest
The question about where to invest to benefit the most from compound interest has become a feature of our email inbox, with people considering mutual funds, ETFs, MMFs and high-yield savings accounts, and wanting to know the advantages and risks.
We at The Calculator Site work to develop quality tools to assist you with your financial calculations. We can't, however, advise you about where to invest your money to achieve the best returns for you. Instead, we advise you to speak to a qualified financial advisor for advice based upon your own circumstances.
There are also some excellent articles from renowned financial websites that list common types of investment for compound interest. Here are two of the best articles, to help with your research:
- Top 11 Compound Interest Investments. Stock Analysis (author: Lincoln Olson).
- Accounts That Earn Compounding Interest. Motley Fool (author: Adam Levy).
How is compound interest calculated?
Now that you understand how powerful compound interest can be, let's break down how it’s calculated. Compound interest works by adding earned interest back to the principal. This generates additional interest in the periods that follow, which accelerates your investment growth.
The formula used for calculating compound interest is:
Where:
- A = the future value of the investment
- P = the principal balance
- r = the annual interest rate (decimal)
- n = number of times interest is compounded per year
- t = the time in years
- ^ = ... to the power of ...
For example, if you want to calculate monthly compound interest, simply divide the annual interest rate by 12 (the number of months in a year), add 1, and raise the result to the power of 12 * t (years).
If you'd prefer not to do the math manually, you can use the compound interest calculator at the top of our page. Simply enter your principal amount, interest rate, compounding frequency and the time period. You can also include regular deposits or withdrawals to see how they impact the future value.
See also: Savings Goal Calculators | Money Market Account Calculator | Loan Calculator
What will $10,000 be worth in 20 years?
We've discussed what compound interest is and how it is calculated. So, let's now break down interest compounding by year, using a more realistic example scenario. We'll say you have $10,000 in a savings account earning 5% interest per year, with annual compounding. We'll assume you intend to leave the investment untouched for 20 years. Your investment calculation might look like this...
| Year | Interest Calculation | Interest Earned | End Balance |
|---|---|---|---|
| Year 1 | $10,000 x 5% | $500 | $10,500 |
| Year 2 | $10,500 x 5% | $525 | $11,025 |
| Year 3 | $11,025 x 5% | $551.25 | $11,576.25 |
| Year 4 | $11,576.25 x 5% | $578.81 | $12,155.06 |
| Year 5 | $12,155.06 x 5% | $607.75 | $12,762.82 |
| Year 6 | $12,762.82 x 5% | $638.14 | $13,400.96 |
| Year 7 | $13,400.96 x 5% | $670.05 | $14,071 |
| Year 8 | $14,071 x 5% | $703.55 | $14,774.55 |
| Year 9 | $14,774.55 x 5% | $738.73 | $15,513.28 |
| Year 10 | $15,513.28 x 5% | $775.66 | $16,288.95 |
| Year 11 | $16,288.95 x 5% | $814.45 | $17,103.39 |
| Year 12 | $17,103.39 x 5% | $855.17 | $17,958.56 |
| Year 13 | $17,958.56 x 5% | $897.93 | $18,856.49 |
| Year 14 | $18,856.49 x 5% | $942.82 | $19,799.32 |
| Year 15 | $19,799.32 x 5% | $989.97 | $20,789.28 |
| Year 16 | $20,789.28 x 5% | $1,039.46 | $21,828.75 |
| Year 17 | $21,828.75 x 5% | $1,091.44 | $22,920.18 |
| Year 18 | $22,920.18 x 5% | $1,146.01 | $24,066.19 |
| Year 19 | $24,066.19 x 5% | $1,203.31 | $25,269.50 |
| Year 20 | $25,269.50 x 5% | $1,263.48 | $26,532.98 |
$10,000 invested at a fixed 5% yearly interest rate, compounded yearly, will grow to $26,532.98 after 20 years. This means total interest of $16,532.98 and a return on investment of 165%.
It's important to remember that these example calculations assume a fixed percentage yearly interest rate. Real-life returns are rarely as predictable as these examples. If you are investing your money, rather than saving it in fixed rate accounts, the reality is that returns on investments will vary year on year due to fluctuations in interest rates, market conditions, inflation, and other economic factors.
It is for this reason that financial experts commonly suggest the risk management strategy of diversification.
Compounding with additional deposits
As we discussed in our section about growth strategies, combining interest compounding with regular deposits into your savings account, Roth IRA, 401(k) or other investment vehicle is a highly efficient saving strategy that can really boost the growth of your money in the longer term.
Looking back at our example from above, if we were to contribute an additional $100 per month into our investment, our balance after 20 years would hit the heights of $67,121, with interest of $33,121 on total deposits of $34,000.
As financial institutions point out, if people begin making regular investment contributions early on in their lives, they can see significant growth in their savings further down the road as their interest snowball gets larger and they gain benefit from Dollar-cost or Pound-cost averaging. 2
Note that you can include regular weekly, bi-weekly (fortnightly), monthly, quarterly or yearly deposits in your calculations with our compound interest calculator at the top of the page.
FAQ
Let's cover some frequently asked questions about our compound interest calculator.
When is my interest compounded?
With savings and investments, interest can be compounded at either the start or the end of the compounding period. If additional deposits or withdrawals are included in your calculation, our calculator gives you the option to include them at either the start or end of each period.
Can I include regular withdrawals?
You can include regular withdrawals within your compound interest calculation as either a monetary withdrawal or as a percentage of interest/earnings. This can be used in combination with regular deposits.
You may, for example, want to include regular deposits whilst also withdrawing a percentage for taxation reporting purposes. Or, you may be considering retirement and wondering how long your money might last with regular withdrawals.
What is the effective annual interest rate?
The effective annual rate (also known as the annual percentage yield) is the rate of interest that you actually receive on your savings or investment after compounding has been factored in.
When interest compounding takes place, the effective annual rate becomes higher than the nominal annual interest rate. The more times the interest is compounded within the year, the higher the effective annual interest rate will be.
What is RoR/TWR?
Within our compound interest calculator results section, you will see either a Rate of Return (RoR) or Time-Weighted Return (TWR) figure for your calculation. You may be wondering what these are, so let's quickly discuss.
The Rate of Return (RoR) reflects the percentage return on your investment over the entire investment term. We calculate it by taking the Initial investment figure away from the Final value and dividing the resulting figure by the Initial investment. 3
If you include regular deposits or withdrawals in your calculation, we switch to provide you with a Time-Weighted Return (TWR) figure. 4
The TWR figure represents the cumulative growth rate of your investment. It is calculated by breaking out each period's growth individually to remove the effects of any additional deposits and withdrawals. The TWR gives you a clearer picture of how your investment might have performed if you hadn't made extra deposits or withdrawn funds, allowing you to better assess its overall performance. You can learn more about TWR in this article by JP Morgan.
If you want to head back up to the calculator results area, you can click the link here. If you have any feedback or questions about the RoR or TWR, please contact us.
A final word
I hope you found this article helpful and that it has shown you how powerful compounding can be – and why Warren Buffett swears by it. By understanding how compound interest works and applying some simple strategies (like starting early, contributing regularly, and choosing the right investment products) you can set yourself up nicely for long-term savings growth as you build toward the future.
As a final note, many of the features in my compound interest calculator have come as a result of user feedback. So, if you have any comments or suggestions, I would love to hear from you.
By Alastair Hazell Updated: December 2, 2025References
- Using online compound interest tools to improve financial literacy, The Journal of Economic Education.
- How to take advantage of compound growth. Canada Life.
- Rate of return. CFI Education Inc.
- How to Use the Time-Weighted Rate of Return (TWR) Formula. Investopedia.
- Warren Buffett. The Giving Pledge.
