Roman Numerals Converter
Disclaimer: Whilst every effort has been made in building our calculator tools, we are not to be held liable for any damages or monetary losses arising out of or in connection with their use. Full disclaimer.
- Roman numerals symbols
- Remembering numerals with mnemonics
- What are common uses for Roman numerals?
- How to convert Roman numerals
- Roman numerals from 1 to 10
- Roman numerals from 10 to 20
- Last 20 years in Roman numerals
- Advanced rules and exceptions
- The origins of Roman numerals
- Converting large numbers
- Example of converting Roman numerals
- Summary
Roman numerals symbols
The whole Roman numbering system uses seven basic symbols:
| Symbol | Value | Latin Name |
|---|---|---|
| I | 1 | unum |
| V | 5 | quinque |
| X | 10 | decem |
| L | 50 | quīnquāgintā |
| C | 100 | centum |
| D | 500 | quingenti |
| M | 1000 | mille |
Note the absence of any symbol for zero. This is partly because the numeral zero is already built into the existing symbols and also for the Romans, numerals were for counting, rather than calculation. In the Roman mind, anything that had a 'zero' value was by definition not a number, and therefore could be expressed by the Latin words nihil or nulla, meaning 'nothing'.
Roman Numerals were used as the standard numbering system until the 14th century, when they began to be replaced by the Hindu-Arabic system of 10 numeric digits which is in use today. 1
Due to the rules of addition and subtraction, the largest number you can form in Roman numerals is 3,999 which is MMMCMXCIX. You can, however, represent bigger numbers by using a horizontal line, or bar, across the top of a number. We discuss this further down our article.
Remembering numerals with mnemonics
To help you remember the seven Roman numerals, you can use a mnemonic device - a learning technique that aids information retention. Here are two popular suggestions:
What are common uses for Roman numerals?
Some of the common uses of Roman numerals in everyday life include use in clock faces, chapter numbering and copyrighting in books, pharmacy prescriptions, and numbered lists. Sometimes dates are given in Roman numerals for the dating of movies and television programmes. Also, some sporting events, such as the Olympics, the Superbowl and Wrestling events use them.
How to convert Roman numerals
With Roman numerals it's not just important to note each numeral itself, but also the order in which they appear. For example, when a smaller number appears infront of a larger number it means that the smaller number should be deducted from the larger one. If the smaller number appears after it, it gets added.
Here are the three basic rules for constructing Roman numbers:
- Always start with the biggest symbol possible in any number (so XV, not VVV, to make 15) and use symbols left to right in decreasing value. Thus 1,666 is written MDCLXVI.
- No symbol should be repeated four or more times, so IV not IIII (but see 'Exceptions' below!).
- To avoid breaching Rule II or to use the lowest number of symbols, a value can be adjusted downwards by placing one lower value symbol (never more than one) in front of it. This is called subtractive notation.
Thus 40 cannot be XXXX but must be XL (50 – 10).
You can see the basic rules in operation in the progressions from one to ten and from ten to twenty.
Roman numerals from 1 to 10
| Roman | Modern | Explanation |
|---|---|---|
| I | 1 | |
| II | 2 | 1+1 = 2 |
| III | 3 | 1+1+1 = 3 |
| IV | 4 | 5-1 = 4 |
| V | 5 | |
| VI | 6 | 5+1 = 6 |
| VII | 7 | 5+1+1 = 7 |
| VIII | 8 | 5+1+1+1 = 8 |
| IX | 9 | 10-1 = 9 |
| X | 10 |
Roman numerals from 10 to 20
| Roman | Modern | Explanation |
|---|---|---|
| X | 10 | |
| XI | 11 | 10+1 = 11 |
| XII | 12 | 10+1+1 = 12 |
| XIII | 13 | 10+1+1+1 = 13 |
| XIV | 14 | 10+5-1 = 14 |
| XV | 15 | 10+5 = 15 |
| XVI | 16 | 10+5+1 = 16 |
| XVII | 17 | 10+5+1+1 = 17 |
| XVIII | 18 | 10+5+1+1+1 = 18 |
| XIX | 19 | 10+10-1 = 19 |
| XX | 20 | 10+10 = 20 |
Last 20 years in Roman numerals
Here are the last 20 years represented by Roman numerals.
| Year | Roman | Year | Roman |
|---|---|---|---|
| 2022 | MMXXII | 2021 | MMXXI |
| 2020 | MMXX | 2019 | MMXIX |
| 2018 | MMXVIII | 2017 | MMXVII |
| 2016 | MMXVI | 2015 | MMXV |
| 2014 | MMXIV | 2013 | MMXIII |
| 2012 | MMXII | 2011 | MMXI |
| 2010 | MMX | 2009 | MMIX |
| 2008 | MMVIII | 2007 | MMVII |
| 2006 | MMVI | 2005 | MMV |
| 2004 | MMIV | 2003 | MMIII |
| 2002 | MMII | 2001 | MMI |
Advanced rules and exceptions
To make things slightly more complicated, the subtractive notation rule (placing a small number in front of a large one to decrease overall value) is itself subject to three sub-rules:
- The subtractive numeral to the left can only be one of the principal numbers, I, X, or C, never one of the 'five' numerals V, L, and D. Of course M, being the biggest numeral, can't be subtracted either.
- You can only use one subtractive number to the left. So 27 must be XXVII, rather than IIIXXX.
- The subtracted number must at least one tenth of the value of the number it is subtracted from. So you can place X to the left of L or C to make 40 or 90 but you can't use X to the left of a D or M to make 490 or 990. In effect, each power of ten has its own group in the total number. So 999 is made up of CM (900) plus XC (90) plus IX (9).
This is, frankly, a severe pain. It means, for example, that 1999 has to be written MCMXCIX rather than MIM. These are the theoretical rules, developed for modern use of Roman numerals. However, over the course of more than two centuries right across Europe, these rules have frequently been cheerfully ignored.
For example, the number eight is frequently expressed IIX on a number of Roman tombs and monuments and in modern dates, such as the 1928 on a Kew Gardens statue expressed MCMXXIIX, rather than the correct MCMXXVIII. Similarly many clocks and some coins use IIII to represent four, rather than the correct IV.
The origins of Roman numerals
Let's discuss the history of Roman numerals a little more. Roman numerals were the standard system of numbering used by the Romans in ancient Rome. Used primarily for counting, they were adapted from the Etruscan numerals system. The original system of numerals used in the classical era was altered slightly in the Middle Ages, resulting in the numeral system that we use today where letters represent values as numerals.
The Etruscan numbering system had five symbols, three of them shared with Roman.
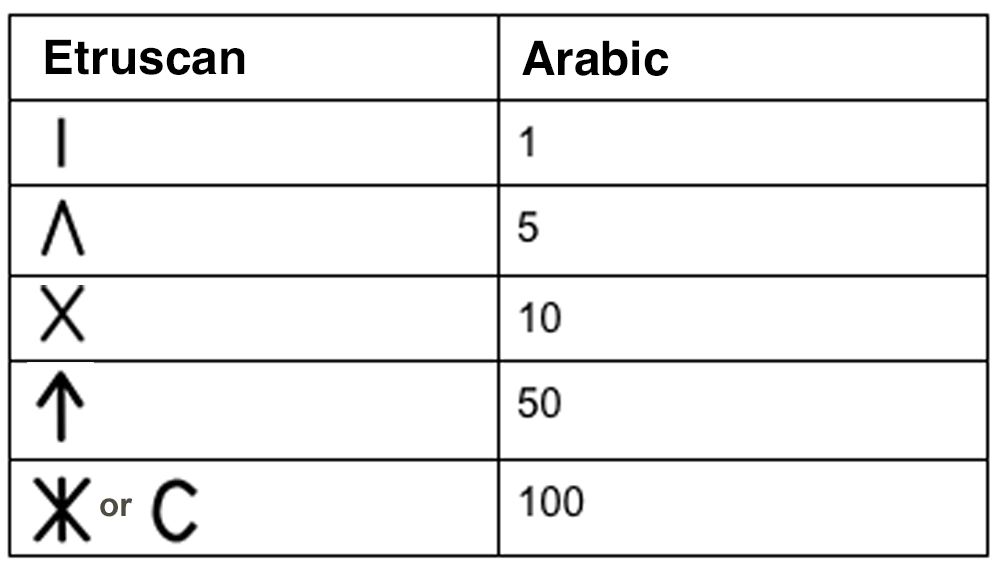
As to how these symbols evolved, there are three main theories.
Theory One: Tally System
The first theory is that the whole numbering system derives from notches on tally sticks, with a single notch (I) representing a single event and every fifth notch double cut (V) and every tenth one cross cut (X). This would have produced the positional system seen in Roman numbering. As for the more advanced symbols, these could have evolved later, being fitted with letters of the Latin alphabet.
Theory Two: Counting on fingers
An alternative hypothesis is that the small numbers in the Roman system are related to hand signals with I, II, III, IIII corresponding to the number of fingers held up for another to see and V representing the whole hand with fingers together and thumb apart. Numbers 6–9 represented one hand held up as a V and the other showing fingers for the additional units and finally a 10 represented by two Vs, crossing the thumbs, or holding both hands up in a cross.Theory Three: Blending symbols
The third theory is that the basic ciphers were I, X, C and Φ for 1, 10, 100 and 1000 and that the ones in between (5, 50, 500) were derived from cutting the basic symbols in half. Thus half an X is a V, half a C is L and half a Φ is D).
These symbols could be used to express any given value, by combining them. Combinations are defined by a set of rules.
Converting large numbers
So how on earth could the Roman numbering system with no zero and no single value above one thousand be used to express a really large number, such as a million? Well, the world was a much smaller place in those days and there would have been less need for really large values.
Nevertheless, one would expect an ingenious and supremely practical people like the Romans to have developed systems to crack that problem and in fact they had two.
Apostrophus
One was to use the apostrophus, a system based on brackets. C|Ɔ represented 1,000 while |Ɔ was 500. Each extra set raised that by a factor of ten. Thus CCC|ƆƆƆ was 100,000 and CCCC|ƆƆƆƆ was a million. Meanwhile |ƆƆƆ represented 50,000 and |ƆƆƆƆ was 500,000.
Therefore to express 15,230 using apostrophi, one would write CC|ƆƆ|ƆƆCCXXX. This breaks down as CC|ƆƆ (10,000) plus |ƆƆ (5,000) plus CC (200) plus XXX (30).
Vinculum
The other large number system was the vinculum, adding lines above and to the sides of conventional Roman numbers, each one multiplying it by 1,000 by adding an overline. Thus V was 5,000, D would be 500,000 while M would be 1,000,000.
| Number | Vinculum | Archaic | Apostrophus |
|---|---|---|---|
| 500 | D | D | |Ↄ |
| 1,000 | M | ↀ | C|Ↄ |
| 5,000 | V | ↁ | |ↃↃ |
| 10,000 | X | ↂ | CC|ↃↃ |
| 50,000 | L | ↇ | |ↃↃↃ |
| 100,000 | C | ↈ | CCC|ↃↃↃ |
| 500,000 | D | |ↃↃↃↃ | |
| 1,000,000 | M | CCCC|ↃↃↃↃ |
Representing large numbers with our converter
Here's how to enter large numbers into our roman numerals calculator. Return to calculator.
| Numeral | Value | How to input |
|---|---|---|
| I | 1,000 | _I |
| V | 5,000 | _V |
| X | 10,000 | _X |
| L | 50,000 | _L |
| C | 100,000 | _C |
| D | 500,000 | _D |
| M | 1,000,000 | _M |
If you want to convert Roman numerals from the apostrophes system to vinculum system, or vice-versa, you can use this converter from ConvertUnits.com.
Example of converting Roman numerals
Let's go through an example of how to convert a set of Roman numerals to their numeric value.

The building in the photograph above is located in Washington D.C and bears the Roman numerals MCMXXII in reference to the fact that it was built in that year (A.D meaning anno Domini, or 'in the year of the Lord'). Our question is, what year do the Roman numerals MCMXXII represent?
- Moving from left to right, we start with the numeral M. M represents 1000.
- The next two numerals are CM. C is 100 and M, as we already know, is 1000. As the C appears before the M, we deduct it from the M. Therefore, 1000 - 100 = 900.
- The remaining numerals go in order. We know that X is 10 and I is 1. So, we have 10+10+1+1.
- Time to add it all together. 1000+900+10+10+1+1 = 1922.
This building therefore appears to have been established in 1922.
Roman numerals charts
The fabulous folks at DadsWorksheets.com have created some great Roman numerals cheat sheets for quick reference of this ancient numbers system. So, do head over there and download them if you want some further conversion practice.
Article summary
- The seven basic Roman numerals are I, V, X, L, C, D, and M (1, 5, 10, 50, 100, 500, and 1,000).
- Roman numerals are written from left to right in decreasing value.
- No symbol should be repeated four or more times. So, it should be IV and not IIII.
- A value can be adjusted downwards by placing one lower value symbol in front of it. E.g: IX (9).
- Large numbers can be represented using the vinculum system. This involves adding a horizontal line over the letter to multiply it by 1000. E.g: V is 5,000 (5 × 1000).
- You can use mnemonics to help remember the order of Roman numerals. I Value Xylophones Like Cows Dig Milk.
If hope the converter and article have been useful to you. If you need any help with converting between Roman numerals and standard numbers, please feel free to make use of the converter at the top of our page.
Calculator: Alastair Hazell.References
- Encyclopedia.com. Roman Numerals: Their Origins, Impact, and Limitations.
- wikiHow. How to Learn Roman Numerals.
- Teaching Roman Numerals. How to Write Roman Numerals.
