Compound Interest Formula With Examples
Compound interest, or "interest on interest", is calculated using the formula A = P(1 + r/n)nt, where P is the principal balance, r is the annual interest rate (as a decimal), n is the number of times interest is compounded per year, and t is the number of years.

The above formula helps you calculate the value of an investment or loan when interest is compounded over time.
Article overview
This guide first appeared on our website in 2014, and over the years we've continued to refine and expand it — adding formula variations, real-world examples, and helpful explanations based on feedback from you, our readers.
Below, we'll walk you through a simple example using the compound interest formula. After that, we'll take a look at variations of the formula for different compounding periods (monthly, quarterly, daily), show you how to use the formula in Excel or Google Sheets and also give examples of formulae that can help you to include monthly deposits.
Here's a quick list of what's to come...
- Sections of guide:
- Quick formula example
- Formula variations
- How to use the formula
- Monthly compound interest formula
- How to use the formula in Excel or Google Sheets
- Example calculation
- Interactive compound interest formula
- Formula for calculating interest rate (%)
- Formula for calculating principal
- Formula for calculating time factor
- Monthly contributions formula
Quick formula example
To better understand how our formula works, let's create a simple example (we'll look into more complex variations, involving different compound intervals and extra contributions, later on in our article). We'll say that you invest $10,000 into a savings account for 20 years at an annual interest rate of 6%, compounded monthly. Here's how our calculation looks:
- P = 10000
- r = 6/100 = 0.06 (decimal)
- n = 12
- t = 20
Plugging those figures into the formula, we can calculate as follows:
- A = 10000 × (1 + 0.06 / 12)(12 × 20)
- A = 10000 × (1 + 0.005)240
- A = 10000 × 3.310204
- A = 33,102.04
The investment balance after 20 years is therefore $33,102.04. If we check this figure using our compound interest calculator, we can see that we have calculated correctly.
Formula variations
To assist those looking for a convenient formula reference, I've included a concise list of compound interest formula variations applicable to common compounding intervals. Later in the article, we will delve into each variation separately for a comprehensive understanding.
| Calculation | Formula |
|---|---|
| Annual compounding (1x compound per year) | A = P(1 + r)t |
| Quarterly compounding | A = P(1 + r/4)4t |
| Monthly compounding | A = P(1 + r/12)12t |
| Daily compounding | A = P(1 + r/365)365t |
| Calculate principal (P) based upon future value | P = A / (1 + r/n)nt |
| Calculate interest rate % (R) | R = n[(A/P)(1/nt)-1] × 100 |
| Calculate time factor (t) | t = ln(A/P) / n[ln(1 + r/n)] |
Where:
- A = future value of the investment/loan
- P = principal amount
- r = annual interest rate (decimal)
- R = annual interest rate (percentage)
- n = number of times interest is compounded per year
- t = time in years
- ln = the natural logarithm
Note on Effective Annual Rates
The formulae listed above are based on the assumption of a nominal annual interest rate (r) divided evenly across the compounding periods. This approach is widely used in financial contexts for simplicity. However, it may result in slight discrepancies in the effective annual rate when transitioning between different compounding intervals (e.g., daily or monthly).
For most purposes, this is considered an acceptable approximation, but if you require precise calculations that ensure the same effective annual rate across all compounding intervals, a more advanced method involving adjustment factors may be needed.
How to use the compound interest formula
In order to use the compound interest formula you will require specific values for your initial balance (principal), annual interest rate (expressed as a decimal), the number of compounds per year and the number of years you wish to calculate for. Let's take a look at how we put these into our formula...
How to calculate compound interest using the formula
Start by multiplying your initial balance by one plus the annual interest rate (expressed as a decimal) divided by the number of compounds per year. Next, raise the result to the power of the number of compounds per year multiplied by the number of years. Subtract the initial balance from the result if you want to see only the interest earned.
The above set out as a formula is:
A = P(1 + r/n)nt
Where:
- A = future value of the investment/loan
- P = principal investment or loan amount
- r = annual interest rate (decimal)
- n = number of times interest is compounded per year
- t = time in years
It's worth noting that this formula gives you the future value of an investment (or loan), which is compound interest plus the principal. Should you wish to calculate the compound interest only, you need to deduct the principal from the result. So, your formula looks like this:
Earned interest only (without principal)
Interest = P(1 + r/n)nt - P
To understand our formula better, let's look at how we can use it for monthly compounding, and we can then go through another example calculation...
Monthly compound interest formula
The formula for calculating compound interest with monthly compounding is:
A = P(1 + r/12)12t
Where:
- A = future value of the investment
- P = principal investment amount
- r = annual interest rate (decimal)
- t = time in years
How to use the formula in Excel or Google Sheets
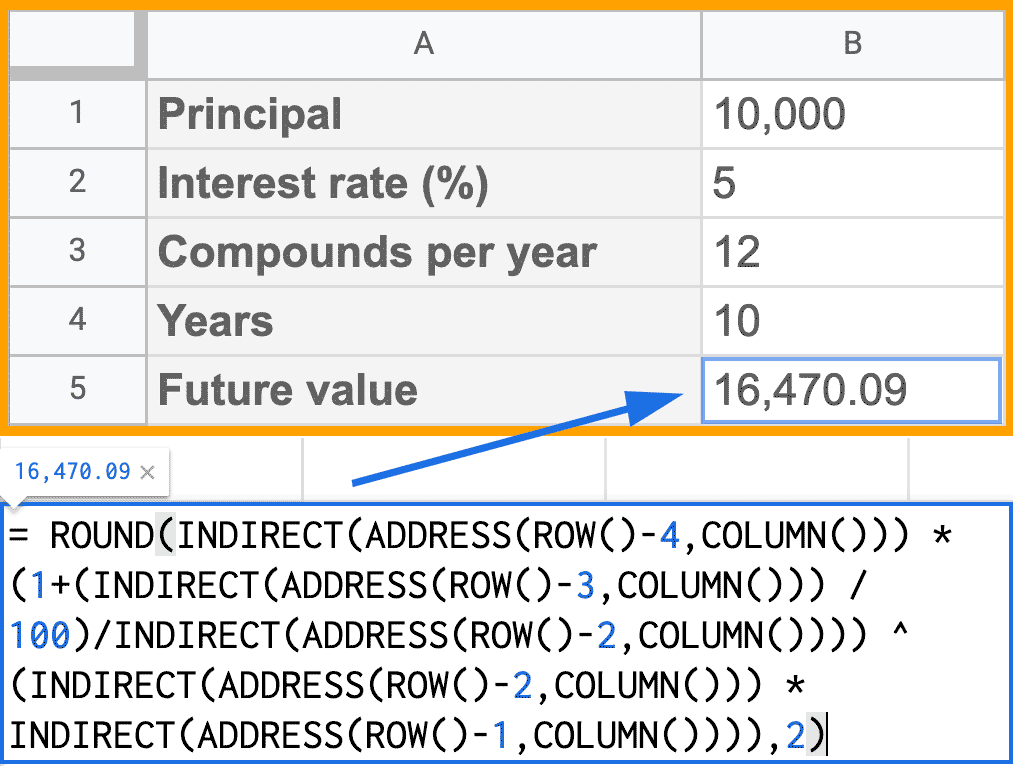
If you're using Excel, Google Sheets or Numbers, you can copy and paste the following into your spreadsheet and adjust your figures for the first four rows as you see fit. This example shows monthly compounding (12 compounds per year) with a 5% interest rate.
| Principal | 10,000 |
| Interest rate (%) | 5 |
| Compounds per year | 12 |
| Years | 10 |
| Future value | = ROUND(INDIRECT(ADDRESS(ROW()-4,COLUMN())) * (1+(INDIRECT(ADDRESS(ROW()-3,COLUMN())) / 100)/INDIRECT(ADDRESS(ROW()-2,COLUMN()))) ^ (INDIRECT(ADDRESS(ROW()-2,COLUMN())) * INDIRECT(ADDRESS(ROW()-1,COLUMN()))),2) |
Here's how it will look in Excel or Google Sheets...
Now that we've looked at how to use the formula for calculations in Excel, here’s an example demonstrating how to use the formula to make a manual calculation...
Example calculation with breakdown
If an amount of $10,000 is deposited into a savings account at an annual interest rate of 3%, compounded monthly, the value of the investment after 10 years can be calculated as follows...
- P = 10000
- r = 3/100 = 0.03 (decimal)
- n = 12
- t = 10
If we plug those figures into the formula, we get the following:
A = 10000 × (1 + 0.03 / 12)(12 * 10) = 13493.54.
So, the investment balance after 10 years is $13,493.54.
Formula methodology
Here’s a step-by-step breakdown of how we get the 13493.54 result. Our methodology revolves around the PEMDAS order of operations. That is to say that we have to perform operations such as multiplication and addition in the right order.
Let's start off with our equation again:
A = 10000 (1 + 0.03 / 12)(12*10)
Using the order of operations we work out the totals in the brackets first.
Within the first set of brackets, you need to do the division first and then the addition (division and multiplication should be carried out before addition and subtraction). We can also work out the 12*10, which is 12 × 10. This gives us...
A = 10000 (1 + 0.0025)120
Then:
A = 10000 (1.0025)120
The exponent goes next. So, we calculate 1.0025120
This means we end up with:
10000 × 1.34935355
= 13,493.54.
The benefits of compound interest
I think it's worth taking a moment to mention the monetary gain that interest compounding can offer.
Looking back at our example, with simple interest (no compounding), your investment balance at the end of the term would be $13,000, with $3,000 interest. With regular interest compounding, however, you would stand to gain an additional $493.54 on top.
Interest for $10,000 at 3% for 10 years:
- With simple interest: $3,000
- With compound interest: $3,493.54
Interest for $10,000 at 5% for 10 years:
- With simple interest: $5,000
- With compound interest: $6,470.09
Interactive compound interest formula
I created the calculator below to show you the formula and resulting accrued investment/loan value (A) for the figures that you enter.
It may be that you want to manipulate the compound interest formula to work out the interest rate for IRR or CAGR, or a principal investment/loan figure. Here are the formulae you need.
Formula for calculating interest rate (r)

This formula can help you work out the yearly interest rate you're getting on your savings, investment or loan. Note that you should multiply your result by 100 to get a percentage figure (%).
r = n[(A/P)(1/nt)-1]
Where:
- r = interest rate (decimal)
- A = future value of the investment
- P = principal investment amount
- n = number of times interest is compounded per year
- t = time in years
Formula for calculating principal (P)

This formula is useful if you want to work backwards and calculate how much your starting balance would need to be in order to achieve a future monetary value.
P = A / (1 + r/n)nt
Where:
- P = principal investment amount
- A = future value of the investment
- r = interest rate (decimal)
- n = number of times interest is compounded per year
- t = time in years
Example: Let's say your goal is to end up with $10,000 in 5 years, and you can get an 8% interest rate on your savings, compounded monthly. Your calculation would be: P = 10000 / (1 + 0.08/12)(12×5) = $6712.10. So, you would need to start off with $6712.10 to achieve your goal.
Formula for calculating time factor (t)
This variation of the formula works for calculating time (t), by using natural logarithms. You can use it to calculate how long it might take you to reach your savings target, based upon an initial balance and interest rate. You can see how this formula was worked out by reading this explanation on algebra.com.
t = ln(A/P) / n[ln(1 + r/n)]
Where:
- A = value of the accrued investment/loan
- P = principal amount
- r = annual interest rate (decimal)
- n = number of times interest is compounded per year
- t = time in years
- ln = the natural logarithm
Monthly contributions formula
I've received a lot of requests over the years to provide a formula for compound interest with monthly contributions. So, let's go over how we do this.
In order to work out calculations involving regular contributions, you will need to combine two formulae: our original compound interest formula — P(1+r/n)(nt) — plus the future value of a series formula for the monthly deposits.
These formulae assume that your frequency of compounding is the same as the periodic payment interval (monthly compounding, monthly contributions, etc).
If you would like to try a version of the formula that allows you to have a different periodic payment interval to the compounding frequency, please see the 'periodic payments' section below.
If the additional deposits are made at the END of the period (end of month, year, etc), here are the two formulae you need:
Compound interest for principal:
\[ \begin{align*} P(1 + \frac{r}{n})^{n \cdot t} \end{align*} \]Future value of a series:
\[ \begin{align*} \text{Total} = PMT \times \left[ \frac{(1 + \frac{r}{n})^{n \cdot t} - 1}{\frac{r}{n}} \right] \end{align*} \]If the additional deposits are made at the BEGINNING of the period (beginning of year, etc), here are the two formulae you need:
Compound interest for principal:
\[ \begin{align*} P(1 + \frac{r}{n})^{n \cdot t} \end{align*} \]Future value of a series:
\[ \begin{align*} \text{Total} = PMT \times \frac{(1 + \frac{r}{n})^{n \cdot t} - 1}{\frac{r}{n}} \color{orange}{\times} (1 + \frac{r}{n}) \end{align*} \]Where:
- A = future value of the investment/loan
- P = principal investment amount
- PMT = monthly payment amount
- r = annual interest rate (decimal)
- n = number of times interest is compounded per year
- t = time in years
Example calculation
If an amount of $5,000 is deposited into a savings account at an annual interest rate of 3%, compounded monthly, with additional deposits of $100 per month (made at the end of each month). The value of the investment after 10 years can be calculated as follows...
P = 5000. PMT = 100. r = 3/100 = 0.03 (decimal). n = 12. t = 10.
Let's plug those figures into our formulae and use our PEMDAS order of operations to create our calculation...
Our investment balance after 10 years therefore works out at $20,720.91.
Calculating different periodic payments
A few people have requested a version of this compound interest formula for future payments that takes into account the number of periodic contributions (both formulae above assume your periodic payments match the frequency of compounding). For example, your money may be compounded daily but you're making contributions monthly.
In this case, you can give the below formula a try. This first version assumes that regular deposits are made at the end of the period (end of the month, end of the quarter, etc).
Compound interest for principal:
\[ \begin{align*} P(1 + \frac{r}{n})^{n \cdot t} \end{align*} \]Future value of a series:
\[ \begin{align*} \text{Total} = PMT \color{orange}{\times} \frac{(1 + \frac{r}{n})^{n \cdot t} - 1} {(1 + \frac{r}{n})^{n / p} - 1} \end{align*} \](With 'p' being the number of periodic payments in the time period)
Example calculation
An amount of $100 is deposited monthly into a savings account at an annual interest rate of 10%, compounded daily. The value of the investment after 12 months can be calculated as follows...
PMT = 100. r = 0.1 (decimal). n = 365 (daily compounding). p = 12 (12 payments). t = 1 (1 year).
Let's plug those figures into our formula...
(Values rounded for clarity; final result calculated using full precision.)
So, the investment balance after 12 months is $1256.79. If we check this against our compound interest calculator we can see the answer is correct.
Should you wish to make payments at the beginning of the period, you need to add (1 + r / n)(n / p) on to the end of the formula, so that it looks like this:
To conclude
This article about the compound interest formula has expanded and evolved based upon your requests for adapted formulae and examples. So, I appreciate it's now quite long and detailed. That said, I hope you've found it useful.
By Alastair Hazell Updated: March 26, 2025Disclaimer: Whilst every effort has been made in building our calculator tools, we are not to be held liable for any damages or monetary losses arising out of or in connection with their use. Full disclaimer.
References
- Discounting and compounding. John A. Dutton e-Education Institute.
If you have any problems using our calculator tool, please contact us.
