BODMAS Explained - Order Of Mathematical Operations
When you're given a sum has two numbers and one operator, calculating an answer seems straightforward (25 × 3 = 75). But, what happens if someone throws in a couple more numbers and operators: (5 + 25 × 3 − 2 = .....)? Which part do you do first? Thankfully, there is a set of simple rules for solving mathematical sums. This is where BODMAS comes in.
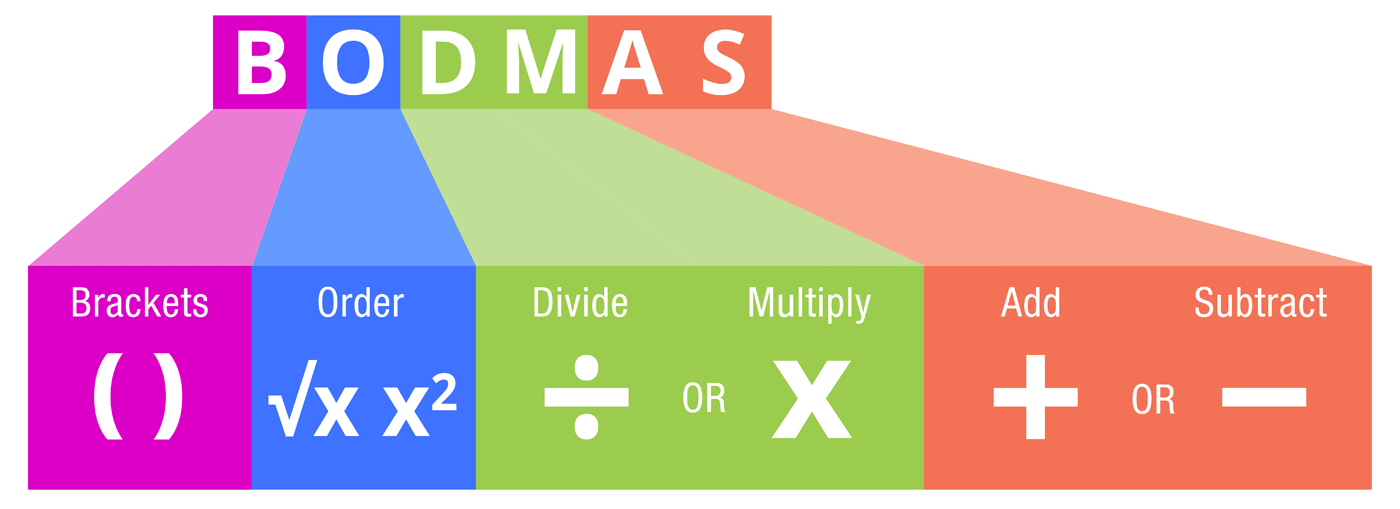
What is BODMAS?
BODMAS is an acronym used in mathematics to represent the order of operations: Brackets, Orders (exponents and roots), Division and Multiplication (from left to right), and Addition and Subtraction (from left to right). It's a guideline for solving mathematical expressions to ensure consistent and accurate results.
BODMAS stands for
- Brackets (any part contained in brackets comes first)
- Order (operations containing powers or square roots)
- Division
- Multiplication
- Addition
- Subtraction
How well known is BODMAS?
In 2012, Dr Peter Price, co-founder of the Classroom Professor website, posted a mathematical question on his Facebook page. This is what he asked:
Can you answer this?
7 - 1 x 0 + 3 ÷ 3 = ?
The post quickly spread around Facebook, with over 70,000 people seeing the post and 6,000 people leaving answers and comments. After 2 weeks, Peter pulled together the results - results that surprised him. Only 26% of respondents gave the correct answer (the correct answer is 8).
When you consider that, psychologically, people are mostly likely to comment on something public like this if they are fairly confident of their answer, so as not to seem foolish, it appears to say a lot about mathematical understanding in the population as a whole. Indeed, it appears to demonstrate that the large majority of people (probably much more than 74%) don't understand the concept of BODMAS and the order of operations.
Sequencing sums: BODMAS
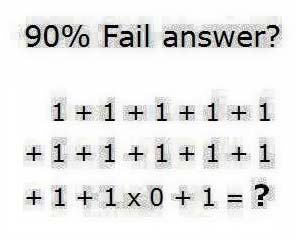
How often have you seen this kind of question doing the rounds on Facebook? The correct answer for this is 12.
In arithmetic, there are two types of components: the numbers themselves and the operators (also called operations) that tell you what to do with those numbers.
So, in the sum 7 x 3 + 5 there are three numbers; 7, 3 and 5 and two operators, a multiplication (x) and an addition (+).You can also see that this sum can produce two different answers depending on which order you use the operators.
- If you multiply seven by three and add five, the answer is 26.
- But if you multiply seven by the sum of three and five (eight), the answer comes out at 56.
So, how do you know in what order to proceed? Trained mathematicians know that there is a definite hierarchy of operations and a default order for performing basic arithmetical operations: adding, subtracting, multiplying and dividing).
BODMAS or PEMDAS?
The definitive order of operations is summed up in the acronym BODMAS, which stands for Brackets, Order, Divide, Multiply, Add, Subtract. It would be easier if BODMAS was recognised worldwide, but unfortunately it isn't.
In the USA it's normally called PEMDAS (Parenthesis, Exponent, Multiply, Divide, Add, Subtract) or PIDMAS (Parenthesis, Index, Divide, Multiply, Add, Subtract). Other places in the world might use BIDMAS (Brackets, Index, Divide, Multiply, Add, Subtract), while Canadians sit in the middle with BEMDAS (Brackets, Exponent, Multiply, Divide, Add, Subtract).
Are BODMAS and PEMDAS the same?
Yes. The acronym terminology may be different, but the sequence remains the same. BODMAS and PEMDAS (and the other similar acronyms) represent an order where multiplication and division are the same step (as with addition and subtraction).

Applying the order of operations
The sequence of the order of operations (whether it be BODMAS, PEMDAS, PIDMAS, BIDMAS or BEMDAS) remains the same:
Step 1: Brackets
The highest level order is defined by anything contained in brackets. These sums are always calculated first. But what if there is more than one set of brackets? The rule then is to start at the innermost set and work outwards. Performing each bracketed calculation should leave you with a single number, allowing that set of brackets to be removed.
Step 2: Order or Index
The terms Order or Index all relate to operations containing powers or indices such as squaring or square rooting. These calculations are all performed second.
Steps 3 and 4: Divide and Multiply
The third and fourth steps, division and multiplication, have equal weight and so form a third level order of operations that are carried out at the same time. Importantly, when two or more operations of the same order appear one-after-another, the operations should be carried out from left to right.
So, if faced with a sum like:
18 ÷ 6 × 4 ÷ 8you just work from left to right. Eighteen over six is three, times four is twelve, divided by eight is 1.5.
Steps 5 and 6: Add and Subtract
Again, these carry equal weight. Therefore the addition and subtractions form the fourth and final level order of operations The third and fourth steps, division and multiplication, have equal weight and so form a third level order of operations that are carried out at the same time, again working from left to right.
In summary, once you have performed all the "B" and "O/E/I" calculations, in that order, just work from left to right doing any "Ds" or "Ms" as you find them, then go back to the beginning and work from left to right on all the "A" or "S" sums.
Using BODMAS - example
How does BODMAS help? If we return to our original sum; 7 x 3 + 5; we can see that there is now only one answer. First perform 7 x 3 as a multiplication (21), followed by the addition of 5 to produce 26. If the intention had been the other way, then it would be necessary to insert brackets, thus: 7 x (3 + 5) so that the bracketed addition is performed first to produce 7 x 8 = 56.
Let's try a much more complex sum to see the whole system in action. To make things easier to spot and differentiate, the division symbols are highlighted in blue and the additions in orange.
Here's a calculation mind-bender:
86 x (15 + 92) - (37 - 18) ÷ ((9 + 9.5) – 8)
---------------------------------------
27 + (15 x 3) x ((72 - 15) x 3.6)
Note that we have two double bracketed calculations. Moreover, the whole sum is a fraction. Where you have double brackets, the inner ones are resolved before the outer ones. In cases where you have an overall fraction type division, the sums are resolved above and below the line, resolving the overall division at the end.
Now, with BODMAS, all this arithmetic becomes straightforward (if somewhat laborious).
Working from the inside outwards, we first resolve all those interior bracketed calculations, producing:
86 x (15 + 92) – (37 – 18) ÷ (18.5 – 8)
---------------------------------------
27 + (15 x 3) x (57 x 3.6)
Then, working left to right, both above and below the line, we resolve all the remaining bracketed calculations:
86 x 107 – 19 ÷ 10.5
---------------------------------------
27 + 45 x 205.2
Now we process the remaining Order operation (86) to give us:
262144 x 107 – 19 ÷ 10.5
---------------------------------------
27 + 45 x 205.2
Next we calculate all the multiplications and divisions above and below the line from left to right. Note that the top line contains an ambiguity similar to the one we met in the beginning. Could it be 262144 x (107 – 19), which produces 23,068,672?
Using the BODMAS formula, however, the multiplications (262144 x 107 and 45 x 205.2) clearly take precedence.
This gives:
28,049,408 – 19 ÷ 10.5
---------------------------------------
27 + 9234
Again, we are left with what would be ambiguities without BODMAS. However, the rules say division takes priority. So we will approach this as:
28049408 – (19 ÷ 10.5)
---------------------------------------
27 + 9234
Applying these, we arrive at:
28049408 – 1.8095
---------------------------------------
27 + 9234
Finally, applying the additions and subtractions, at:
28049406.1905
---------------------------------------
9261
At last, we are left with an overall division that resolves into a final answer (rounded up to three decimal places) of:
3028.766
Special cases
There aren't really any exceptions to the BODMAS hierarchy but there are a couple of special cases involving orders or exponents.
The first is where you get an exponent inside a bracketed part of the calculation, such as:
25 + (5 × 82 + 7)
Although brackets theoretically take precedence over orders, within the bracketed part of the sum, the exponent takes priority over everything else so we resolve that first.
25 + (5 × 64 + 7)
Similarly, within the brackets, the multiplication now takes priority, so:
25 + (320 + 7)
Now the addition to let us dispense with the brackets:
25 + 327
Final answer: 352
Exponents
There is one last special case, involving exponents of exponents.
Just occasionally you might come across a calculation containing something like this:
723
In other words, seven raised to the power of two cubed.
In this case only, we break the left to right rule to work from right to left or from the outside inwards.
First, resolve the cube of two, which is: 2 x 2 x 2 = 8Now move left again, to work out seven to the power of eight. We need to be careful here and understand that 'exponent' means how many times to use the base number in multiplication by itself.
So in seven to the power eight (78) , seven is the 'base' - the thing being multiplied - and eight is the exponent, how many times it's used.
It's quite easy - and I made exactly this mistake in a former draft of this article - to repeat the basic operation 7x7 eight times to produce 40,353,607. WRONG!
What this overlooks is that the first seven is not only the base but also the first exponent. 71 (seven to the power of one) is... seven.
Thus the first multiplication (7x7) is 72 or seven squared. Therefore 78 can be mapped as:
7 = seven to the power of one
7x7 = 49 (seven to power of 2)
49 x 7 = 343 (seven to power of 3)
343 x 7 = 2401 (seven to power of 4)
2401 x 7 = 16807 (seven to power of 5)
16807 x 7 = 117649 (seven to power of 6)
117649 x 7 = 823543 (seven to power of 7)
823543 x 7 = 5764801 (seven to power of 8)
So the final answer to that complex multiple operations PEDMAS sum is:
5,764,801
And that, Ladies and Gentlemen, is how we do that.
Placing brackets
A couple of things should be clear from all this. Firstly, you need brackets in complex calculations. The brackets are your navigational waypoints through the sum.
Secondly, get the placement of those brackets wrong and you will end up with the wrong answer. Maths is very unforgiving that way.
Therefore, and finally, complex sums need to be designed and mapped out like complicated journeys. Before getting your trusty calculator out, you will probably need to sketch the whole sum out on paper, to make sure all your ducks (or brackets) are nicely lined up in a row before you begin the actual calculation.
A BODMAS test
Have you been concentrating? It's time to find out, with a little question designed to test your understanding of BODMAS and the order of operations.
Have a go at the question below. There's no prize, other than the bragging rights of being top of the class (you boffin!).
Happy BODMAS!
