Cubic Feet Calculator
- Square Footage
- Cubic Feet
- CBM
- Cubic Yards
Use this free cubic feet calculator to calculate the cubic feet volume of a box, space, container or appliance using width, length, height, or area measurements. Convert from feet, inches, meters, cm, yards, or square feet.
Disclaimer: Whilst every effort has been made in building our calculator tools, we are not to be held liable for any damages or monetary losses arising out of or in connection with their use. Full disclaimer.
How to calculate cubic feet
To calculate the cubic feet volume or capacity of an item or space, measure the length, width and height in feet and then multiply the measurements together: length × width × height.
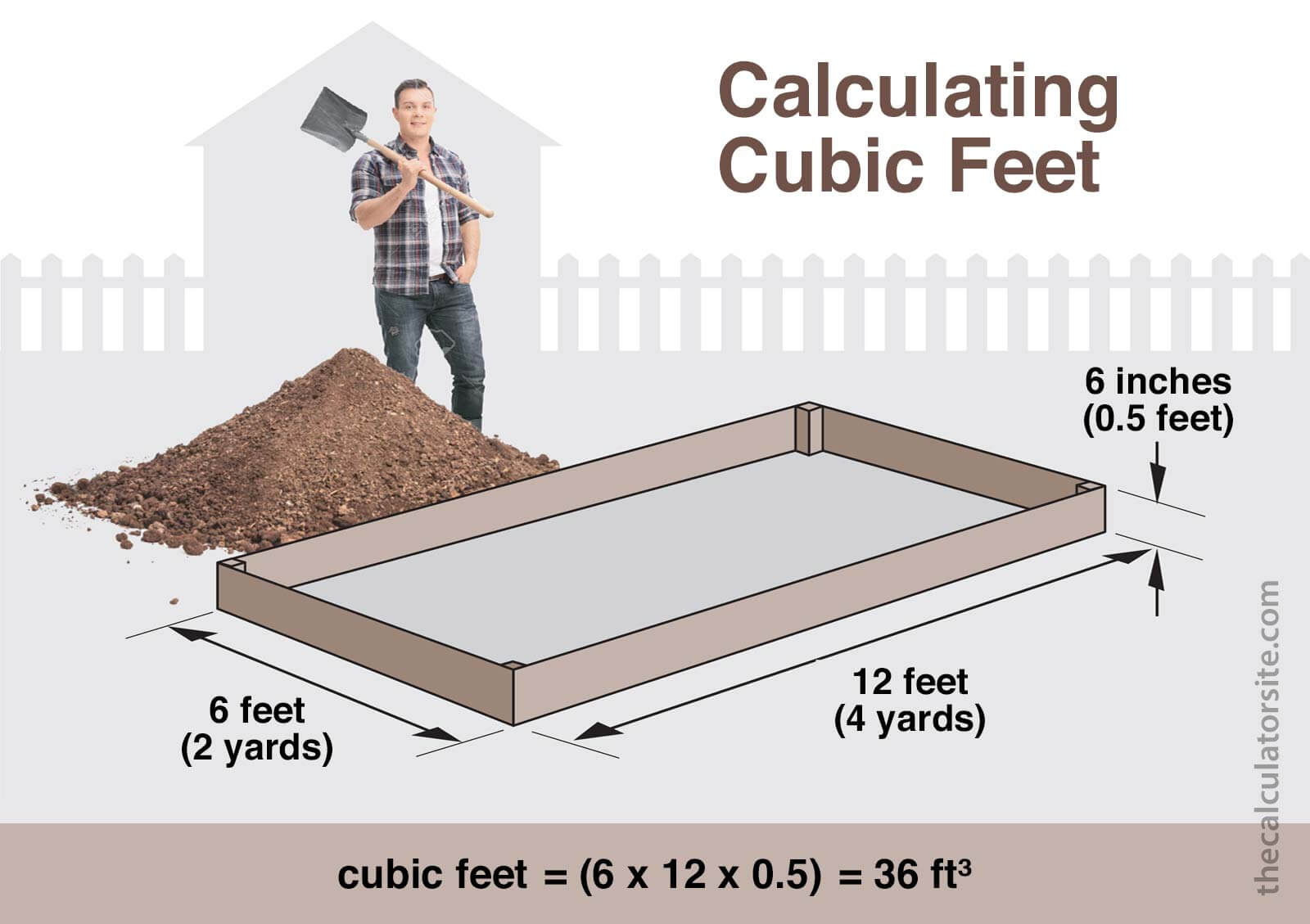
It's not an everyday problem, but there will be times when you need to calculate the capacity of something. Instead of staring blankly into the trunk of your car, getting a tension headache trying to find the biggest bathtub, or weeping when confronted by the decision over buying a new fridge-freezer or oven, just take control!
There are only three measurements you need to take to work out the volume or capacity in cubic feet: length, width and height. It's worth being aware of the object you're measuring, however.
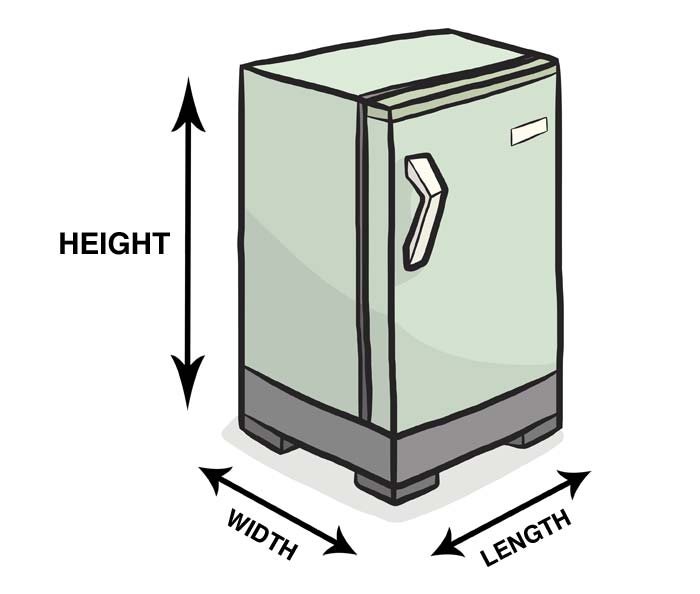
For example, if you're aiming to measure the cubic feet capacity of a refrigerator, you need to measure the space inside the fridge, and not the dimensions of the exterior. You can read instructions for measuring a refrigerator here.
Once you've obtained the three measurements, it's only a case of multiplying them together.
Calculating irregular shapes
If the shape is irregular, mentally divide it into regular shapes and calculate the volume for each part separately, before adding them all together.
For example, an L shaped cabinet designed to fit the corner of a room could be dealt with as two different rectangles, one longer, one shorter. Just work out the capacity of each one individually and then add them together for the total capacity of the cabinet.

Converting from units other than feet
If you're shopping online, the dimensions of something may only be given in inches. If you're looking at plans for a room, maybe the figures are given in meters or yards. But don't worry! To arrive at the cubic feet measurement, you only need to add one extra step into your calculations...
- If you need to convert to cubic feet from inches: divide the final number (i.e. the total you get after multiplying the three dimensions together) by 1728.
- If you need to convert to cubic feet from meters/metres: multiply your final number by 35.31.
- If you need to convert to cubic feet from yards: multiply your final number by 27.
If you have a figure in square feet and want to convert to cubic feet, you can simply multiply it by your height measurement. Or, you can use our conversion tool
Let's go through the individual calculations one at a time...
Calculating cubic feet from inches
If you have measured the dimensions of your item in inches then do the following:
- Multiply your length, width and height figures together, giving you a total in cubic inches (in³)
- Divide the total by 1728 (as there are 1728 cubic inches in a cubic foot).
Inches to cubic feet example
Let's say you're looking for the capacity of a refrigerator that measures 64" x 28" x 29" inside. Here's the process...
- Multiply your inches measurements together: 64 x 28 x 29 = 51968 cubic inches.
- Divide the result by 1728: 51968 / 1728 = 30.074 cu ft.
You can then check your answer against the calculator at the top of the page. We'll look at some more real world calculation examples later in this article.
Calculating cubic feet from meters
If you have measured the dimensions of your item in meters then do the following:
- Multiply your length, width and height figures together, giving you a total in cubic meters (cbm)
- Multiply the total by 35.31.
Calculating cubic feet from yards
If you have measured the dimensions of your item in yards then do the following:
- Multiply your length, width and height figures together, giving you a total in cubic yards (yd³)
- Multiply the total by 27 (as there are 27 cubic feet in a cubic yard).
Once you've calculated your result, you can check it against the calculator at the top of this page. You may then wish to convert your figure to gallons if you're going to be ordering a quantity of material or liquid.
How to convert from cubic inches to cubic feet
One cubic foot equals 1728 cubic inches. To convert from cubic inches to cubic feet, divide your cubic inches figure by 1728. If you don't want to do this manually, give the volume converter a try.
Real world examples
Let's take a look at a couple of examples of situations where you may need to calculate cubic feet...
Example 1
I want to buy a dressing-up box for my daughter, but one looks longer while the other looks taller. I can't judge by eye which one can store the most costumes.
Box A is 70" x 30" x 30" = 63,000".
63,000 divided by 1728 (cubic inches to cubic ft conversion) = 36.45. So it is 36.45ft³
Box B is 60" x 28" x 45" = 75,600".
75,600 divided by 1728 (cubic inches to cubic ft conversion) = 43.75.
So it is 43.75ft³. Box B has the larger capacity, so I will buy that one.
Let's try another...
Example 2
My friend is driving us on a trip, and I need to work out how much stuff I can bring.
The trunk of her car is L shaped, because there's a storage section built into one corner to hold a toolbox. The largest rectangle of the L is 60" x 30" x 35" and the smaller rectangle is 18" x 14" x 35".
Larger rectangle
60 x 30 x 35 = 63,000.
63,000 divided by 1728 = 36.45.
36.45ft³
Smaller rectangle
18 x 14 x 35 = 8,820.
8,820 divided by 1728 = 5.10.
5.10ft³
And the two added together (36.45ft³ + 5.1ft³ ) makes a total capacity of 41.55ft³.
To check your calculations, we recommend making use of the cubic feet calculator at the top of the page.
Calculator by Alastair HazellIf you have any problems using our cubic feet calculator, please contact us.
